若集合 ,则
( )
A . B .
C .
D .
若 ,则
( )
A . B .
C . 1 D . 2
在 中,点 D 在边 AB 上,
.记
,则
( )
A . B .
C .
D .
南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库 . 已知该水库水位为海拔 时,相应水面的面积为
;水位为海拔
时,相应水面的面积为
,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔
上升到
时,增加的水量约为(
)( )
A . B .
C .
D .
从 2 至 8 的 7 个整数中随机取 2 个不同的数,则这 2 个数互质的概率为( )
A . B .
C .
D .
记函数 的最小正周期为 T .若
,且
的图象关于点
中心对称,则
( )
A . 1 B . C .
D . 3
设 ,则( )
A . B .
C .
D .
已知正四棱锥的侧棱长为 l ,其各顶点都在同一球面上 . 若该球的体积为 ,且
,则该正四棱锥体积的取值范围是( )
A . B .
C .
D .
已知正方体 ,则( )
A .直线 与
所成的角为
B .直线
与
所成的角为
C .直线 与平面
所成的角为
D .直线
与平面 ABCD 所成的角为
已知函数 ,则( )
A . 有两个极值点 B .
有三个零点
C .点 是曲线
的对称中心 D .直线
是曲线
的切线
已知 O 为坐标原点,点 在抛物线
上,过点
的直线交 C 于 P , Q 两点,则( )
A . C 的准线为 B .直线 AB 与 C 相切
C . D .
已知函数 及其导函数
的定义域均为
,记
,若
,
均为偶函数,则( )
A . B .
C .
D .
的展开式中
的系数为 (用数字作答).
写出与圆 和
都相切的一条直线的方程 .
若曲线 有两条过坐标原点的切线,则 a 的取值范围是 .
已知椭圆 , C 的上顶点为 A ,两个焦点为
,
,离心率为
.过
且垂直于
的直线与 C 交于 D , E 两点,
,则
的周长是 .
记 为数列
的前 n 项和,已知
是公差为
的等差数列.
(1) 求 的通项公式;
(2) 证明: .
记 的内角 A , B , C 的对边分别为 a , b , c ,已知
.
(1) 若 ,求 B ;
(2) 求 的最小值.
如图,直三棱柱 的体积为 4 ,
的面积为
.
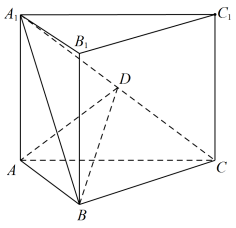
(1) 求 A 到平面 的距离;
(2) 设 D 为 的中点,
,平面
平面
,求二面角
的正弦值.
一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两类)的关系,在已患该疾病的病例中随机调查了 100 例(称为病例组),同时在未患该疾病的人群中随机调查了 100 人(称为对照组),得到如下数据:
| | 不够良好 | 良好 |
| 病例组 | 40 | 60 |
| 对照组 | 10 | 90 |
(1) 能否有 99% 的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异?
(2) 从该地的人群中任选一人, A 表示事件 “ 选到的人卫生习惯不够良好 ” , B 表示事件 “ 选到的人患有该疾病 ” . 与
的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为 R .
( ⅰ )证明: ;
( ⅱ )利用该调查数据,给出 的估计值,并利用( ⅰ )的结果给出 R 的估计值.
附 ,
| | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
已知点 在双曲线
上,直线 l 交 C 于 P , Q 两点,直线
的斜率之和为 0 .
(1) 求 l 的斜率;
(2) 若 ,求
的面积.
已知函数 和
有相同的最小值.
(1) 求 a ;
(2) 证明:存在直线 ,其与两条曲线
和
共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.