若 ，则 （ ）

A ． B ． C ． D ．

某社区通过公益讲座以普及社区居民的垃圾分类知识．为了解讲座效果，随机抽取 10 位社区居民，让他们在讲座前和讲座后各回答一份垃圾分类知识问卷，这 10 位社区居民在讲座前和讲座后问卷答题的正确率如下图：

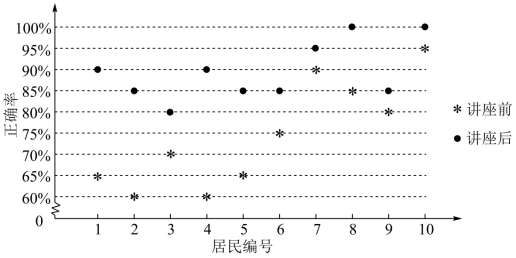
则（ ）

A ．讲座前问卷答题的正确率的中位数小于

B ．讲座后问卷答题的正确率的平均数大于

C ．讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差

D ．讲座后问卷答题的正确率的极差大于讲座前正确率的极差

设全集 ，集合 ，则 （ ）

A ． B ． C ． D ．

如图，网格纸上绘制的是一个多面体的三视图，网格小正方形的边长为 1 ，则该多面体的体积为（ ）

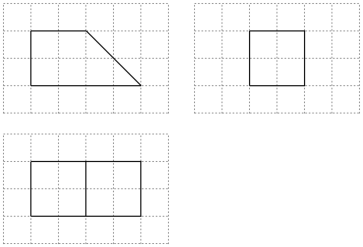
A ． 8 B ． 12 C ． 16 D ． 20

函数 在区间 的图象大致为（ ）

A 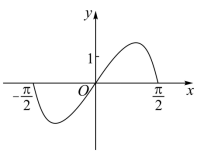． B ．

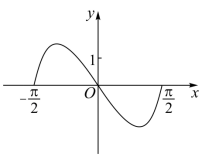C ． D ．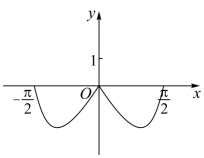

当 时，函数 取得最大值 ，则 （ ）

A ． B ． C ． D ． 1

在长方体 中，已知 与平面 和平面 所成的角均为 ，则（ ）

A ． B ． AB 与平面 所成的角为

C ． D ． 与平面 所成的角为

沈括的《梦溪笔谈》是中国古代科技史上的杰作，其中收录了计算圆弧长度的 “ 会圆术 ” ，如图， 是以 O 为圆心， OA 为半径的圆弧， C 是 AB 的中点， D 在 上， ． “ 会圆术 ” 给出 的弧长的近似值 s 的计算公式： ．当 时， （ ）

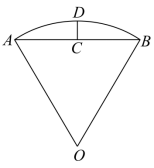
A ． B ． C ． D ．

甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为 ，侧面积分别为 和 ，体积分别为 和 ．若 ，则 （ ）

A ． B ． C ． D ．

椭圆 的左顶点为 A ，点 P ， Q 均在 C 上，且关于 y 轴对称．若直线 的斜率之积为 ，则 C 的离心率为（ ）

A ． B ． C ． D ．

设函数 在区间 恰有三个极值点、两个零点，则 的取值范围是（ ）

A ． B ． C ． D ．

已知 ，则（ ）

A ． B ． C ． D ．

设向量 ， 的夹角的余弦值为 ，且 ， ，则 ．

若双曲线 的渐近线与圆 相切，则 ．

从正方体的 8 个顶点中任选 4 个，则这 4 个点在同一个平面的概率为 ．

已知 中，点 D 在边 BC 上， ．当 取得最小值时， ．

记 为数列 的前 n 项和．已知 ．

(1) 证明： 是等差数列；

(2) 若 成等比数列，求 的最小值．

在四棱锥 中， 底面 ．

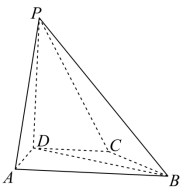
(1) 证明： ；

(2) 求 PD 与平面 所成的角的正弦值．

甲、乙两个学校进行体育比赛，比赛共设三个项目，每个项目胜方得 10 分，负方得 0 分，没有平局．三个项目比赛结束后，总得分高的学校获得冠军．已知甲学校在三个项目中获胜的概率分别为 0.5 ， 0.4 ， 0.8 ，各项目的比赛结果相互独立．

(1) 求甲学校获得冠军的概率；

(2) 用 X 表示乙学校的总得分，求 X 的分布列与期望．

设抛物线 的焦点为 F ，点 ，过 F 的直线交 C 于 M ， N 两点．当直线 MD 垂直于 x 轴时， ．

(1) 求 C 的方程；

(2) 设直线 与 C 的另一个交点分别为 A ， B ，记直线 的倾斜角分别为 ．当 取得最大值时，求直线 AB 的方程．

已知函数 ．

(1) 若 ，求 a 的取值范围；

(2) 证明：若 有两个零点 ，则 ．

在直角坐标系 中，曲线 的参数方程为 （ t 为参数），曲线 的参数方程为 （ s 为参数）．

(1) 写出 的普通方程；

(2) 以坐标原点为极点， x 轴正半轴为极轴建立极坐标系，曲线 的极坐标方程为 ，求 与 交点的直角坐标，及 与 交点的直角坐标．

已知 a ， b ， c 均为正数，且 ，证明：

(1) ；

(2) 若 ，则 ．