集合 ,则
( )
A . B .
C .
D .
设 ,其中
为实数,则( )
A . B .
C .
D .
已知向量 ,则
( )
A . 2 B . 3 C . 4 D . 5
分别统计了甲、乙两位同学 16 周的各周课外体育运动时长(单位: h ),得如下茎叶图:
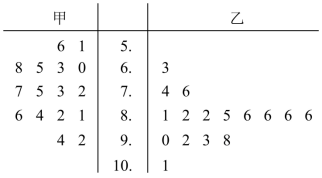
则下列结论中错误的是( )
A .甲同学周课外体育运动时长的样本中位数为 7.4
B .乙同学周课外体育运动时长的样本平均数大于 8
C .甲同学周课外体育运动时长大于 8 的概率的估计值大于 0.4
D .乙同学周课外体育运动时长大于 8 的概率的估计值大于 0.6
若 x , y 满足约束条件 则
的最大值是( )
A . B . 4 C . 8 D . 12
设 F 为抛物线 的焦点,点 A 在 C 上,点
,若
,则
( )
A . 2 B . C . 3 D .
执行下边的程序框图,输出的 ( )
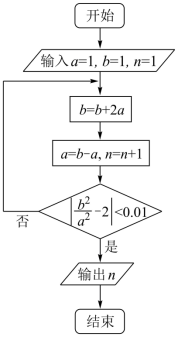
A . 3 B . 4 C . 5 D . 6
如图是下列四个函数中的某个函数在区间 的大致图像,则该函数是( )
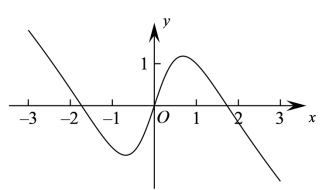
A . B .
C .
D .
在正方体 中, E , F 分别为
的中点,则( )
A .平面 平面
B .平面
平面
C .平面 平面
D .平面
平面
已知等比数列 的前 3 项和为 168 ,
,则
( )
A . 14 B . 12 C . 6 D . 3
函数 在区间
的最小值、最大值分别为( )
A . B .
C .
D .
已知球 O 的半径为 1 ,四棱锥的顶点为 O ,底面的四个顶点均在球 O 的球面上,则当该四棱锥的体积最大时,其高为( )
A . B .
C .
D .
记 为等差数列
的前 n 项和.若
,则公差
.
从甲、乙等 5 名同学中随机选 3 名参加社区服务工作,则甲、乙都入选的概率为 .
过四点 中的三点的一个圆的方程为 .
若 是奇函数,则
,
.
记 的内角 A , B , C 的对边分别为 a , b , c ﹐已知
.
(1) 若 ,求 C ;
(2) 证明:
如图,四面体 中,
, E 为 AC 的中点.
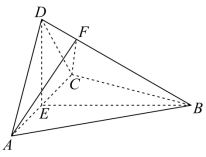
(1) 证明:平面 平面 ACD ;
(2) 设 ,点 F 在 BD 上,当
的面积最小时,求三棱锥
的体积.
某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了 10 棵这种树木,测量每棵树的根部横截面积(单位: )和材积量(单位:
),得到如下数据:
| 样本号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 总和 |
| 根部横截面积 | 0.04 | 0.06 | 0.04 | 0.08 | 0.08 | 0.05 | 0.05 | 0.07 | 0.07 | 0.06 | 0.6 |
| 材积量 | 0.25 | 0.40 | 0.22 | 0.54 | 0.51 | 0.34 | 0.36 | 0.46 | 0.42 | 0.40 | 3.9 |
并计算得 .
(1) 估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量;
(2) 求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到 0.01 );
(3) 现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为 .已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值.
附:相关系数 .
已知函数 .
(1) 当 时,求
的最大值;
(2) 若 恰有一个零点,求 a 的取值范围.
已知椭圆 E 的中心为坐标原点,对称轴为 x 轴、 y 轴,且过 两点.
(1) 求 E 的方程;
(2) 设过点 的直线交 E 于 M , N 两点,过 M 且平行于 x 轴的直线与线段 AB 交于点 T ,点 H 满足
.证明:直线 HN 过定点.
在直角坐标系 中,曲线 C 的参数方程为
,( t 为参数),以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,已知直线 l 的极坐标方程为
.
(1) 写出 l 的直角坐标方程;
(2) 若 l 与 C 有公共点,求 m 的取值范围.
已知 a , b , c 都是正数,且 ,证明:
(1) ;
(2) ;